量子力学导论

波粒二象性

1. 光子能量: E = hν = ℏω

2. 光子动量:

3. de Broglie 波长:

4. 不确定关系:

5. 常用相对论能量-动量关系 E² = p²c² + m₀²c⁴ E = E_K + m₀c²

可得出E_k的两种表达*： 1. 用速度 v表示： 2. 用动量 p表示：

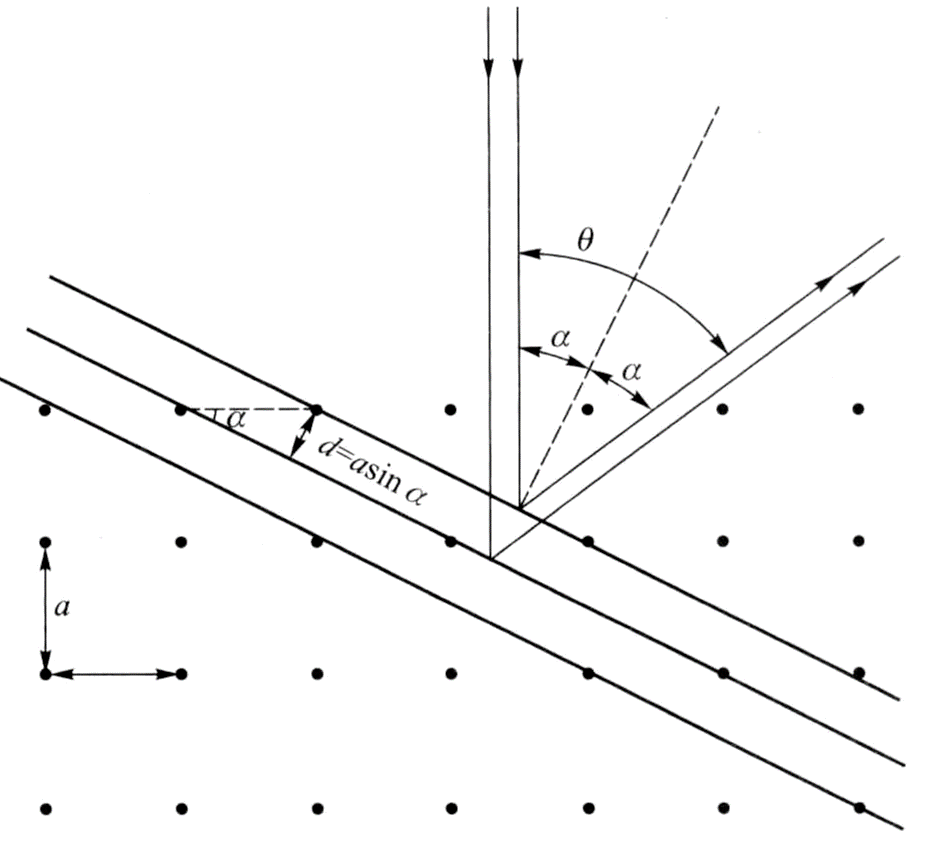
德布罗意波的实验验证——戴维逊-革末实验

布拉格公式： 2dsin θ = nλ d：晶体中相邻原子层（晶面）的间距（晶面间距）。 θ：入射波与晶面的夹角，称为掠射角（入射角的余角，即入射方向与晶面的夹角）。

应用于本例，布拉格衍射的晶格常数为 a，入射与出射方向的夹角为 θ ，则强波束射出的条件是 nλ = asin θ

在非相对论近似下，

当入射电子能量E_k = 54eV时，可算得 λ = 0.167nm。进而

对于镍晶体，晶格常数a = 0.215nm ，若取入射电子能量E = 54eV ，则

sin θ = 0.776n

波函数

单值、连续、可微、归一化——是量子力学中为了描述粒子状态并确保物理理论的合 理性而提出的数学要求。

1. 波函数: ψ(r, t) = ψ₀e^{i(k ⋅ r − ωt)}
2. 统计诠释: P = |ψ(r, t)|²dV
3. 归一化条件: ∫_−∞^+∞|ψ(r, t)|²dV = 1 4.态叠加原理： ψ(r, t) = ψ₁(r, t) + ψ₂(r, t) |ψ(r, t)|² = ψ(r, t)ψ^*(r, t) ## Schrodinger 方程

Schrodinger 方程的建立

1. 电磁波的波动方程: (ʲ − c²p̂)ψ(r, t) = 0

2. 相对论 Schrodinger 方程:

   1. Klein-Gordon 方程: E² = p²c² + m₀²c⁴

2. Dirac 方程: E = αcp + βm₀c²

3. 非相对论 Schrodinger 方程: (1) 一维 Schrodinger 方程: (2) 三维 Schrodinger 方程: ### 定态 Schrodinger 方程 定态是体系的一种特殊状态，即能量本征态。

1. 势场不显含时间，Schrodinger 方程变为：
2. 分离变量： ψ(r, t) = ψ(r)T(t)

3. 时间部分： T(t) = T₀e^−iEt/ℏ 这里的相位因子e^−iEt/ℏ描述了波函数随时间的周期性振荡. 相位的变化速率与能量直接相关，这反映了量子系统中的能量－时间关系.

4. 定态波函数： ψ(r, t) = ψ(r)e^−iEt/ℏ

5. 空间部分即定态 Schrodinger 方程： ### Schrodinger 方程的应用

6. 一维无限深势阱：

   1. Schrodinger 方程：

ψ(x) = Asin kx + Bcos kx (2) 边界条件： B = 0,  ka = nπ,  n = 1, 2, … (3) 波函数： (4) 能量： 2. 一维有限深势阱：束缚态(1) 当时，

ψ(x) = Asin kx + Bcos kx (2) 当时，

(3) 势是偶函数，仅讨论偶函数解 (4) 边界条件: De^−k′a = Bcos ka,   − k^′De^−k′a = −kBsin ka

k^′ = ktan ka 3. 方势垒的隧道效应: (1) 当时,

ψ₁(x) = Ae^ik₁x + Be^−ik₁x (2) 当时,

ψ₂(x) = Ce^k₂x + De^−k₂x (3) 当时，没有入射波ψ₃(x) = Fe^ik₁x + Ge^−ik₁x (4) 透射概率:

如果，透射概率可以近似为

5. 反射概率:

一维谐振子

• 哈密顿算符: 其中 是系统的固有角频率。
• 定态薛定谔方程:

- 无量纲变量: 方程变为：

能量本征值与波函数

• 能量本征值:
• 归一化的本征函数:

其中 H_n(ξ) 是厄米多项式。

算符与力学量

算符与对易关系

1. 算符:
   1. Hamilton 算符:
   2. 动量算符: p̂ = −iℏ∇
   3. 能量算符:
   4. 轨道角动量算符: L̂_x = yp̂_z − zp̂_y,  L̂_y = zp̂_x − xp̂_z,  L̂_z = xp̂_y − yp̂_x

L̂² = L̂_x² + L̂_y² + L̂_z² 球坐标下，

2. 正则对易关系:

   1. 坐标与动量的对易关系: [x̂_α, p̂_β] = iℏδ_αβ

   2. 动量算符的对易关系: [p̂_α, p̂_β] = 0

   3. 坐标与角动量的对易关系: [x̂_α, L̂_β] = ε_αβγiℏx̂_γ

   4. 动量与角动量的对易关系: [p̂_α, L̂_β] = ε_αβγiℏp̂_γ

   5. 角动量算符的对易关系: [L̂_α, L̂_β] = ε_αβγiℏL̂_γ

[L̂², L̂] = 0

3. 本征方程: Ôf_n = λ_nf_n 一个本征值对应于个本征函数，称这一本征函数是度简并的。

表象与力学量的平均值

1. 表象与表象变换

在量子力学中，表象是指用一组完备的正交归一基底来描述量子系统的状态和力学量。不同的表象对应于不同的基底，但物理本质是相同的。

• 位置表象：基底是位置本征态 |x⟩，态矢量在位置表象中的表示为波函数 ψ(x) = ⟨x|ψ⟩。
• 动量表象：基底是动量本征态 |p⟩，态矢量在动量表象中的表示为波函数 φ(p) = ⟨p|ψ⟩。
• 能量表象：基底是哈密顿量的本征态 |E_n⟩，态矢量在能量表象中的表示为系数 c_n = ⟨E_n|ψ⟩。

不同表象之间的转换可以通过幺正变换实现。例如，从位置表象到动量表象的转换可以通过傅里叶变换实现： 反之，从动量表象到位置表象的转换为：

2. 力学量的平均值

对于一个力学量 A，其算符为 Â，在态 |ψ⟩ 下的平均值定义为： ⟨A⟩ = ⟨ψ|Â|ψ⟩

• 在位置表象中：如果态矢量 |ψ⟩ 在位置表象中的表示为波函数 ψ(x) = ⟨x|ψ⟩，则其的平均值可以表示为： ⟨A⟩ = ∫_−∞^∞ψ^*(x)Âψ(x)dx
• 在动量表象中：如果态矢量 |ψ⟩ 在动量表象中的表示为波函数 φ(p) = ⟨p|ψ⟩，则其平均值可以表示为： ⟨A⟩ = ∫_−∞^∞φ^*(p)Âφ(p)dp

例如位置算符 x 的平均值： ⟨x⟩ = ∫_−∞^∞ψ^*(x)xψ(x)dx.

动量算符 p 的平均值：

力学量有确定值的条件

厄米算符的性质

在量子力学中，所有可观测量（如位置、动量、能量等）都由厄米算符描述。一个算符 Â 如果满足以下条件，则称为厄米算符：

∫ψ^*Âϕdx = ∫(Âψ)^*ϕdx 对于任意两个波函数 ψ 和 ϕ。

• 厄米算符的本征值为实数：假设厄米算符 Â 的本征函数为 {ϕ_n}，对应本征值为 {λ_n}，则有 λ_n^* = λ_n
• 不同本征值的本征函数具有正交归一性：即 ∫ϕ_k^*ϕ_ldx = δ_kl

力学量具有确定值的条件

1. 当体系处于力学量 A 的本征态时，即 Âϕ = λϕ，对 A 进行测量，将会以100%的概率得到确定值 λ，这也是系统的平均值。

2. 如果体系不是处于本征态而是任意一个叠加态 ψ(x) = ∑_nc_nϕ_n(x)，其中 {ϕ_n} 构成完全系，对应本征值为 {λ_n}。通过计算系数 c_n 可知，测得 λ_n 的概率为 |c_n|²。(洪恩规则)

3. 不同力学量同时有确定值： 当体系处于波函数ψ(x)（Â, B̂ 本征波函数的叠加态）所描写的状态时，测量力学量A、B所得的值，必定是算符Â, B̂的本征值之一，测得λ_n, μ_n的概率为|c_n|²

推论：一组算符{Â₁, Â₂, ⋯}有共同本征函数且构成完全系，它们同时有确定值。相应地，这组物理量对应的算符中的任何两个都互相对易。

守恒量

如果物理量的算符 Â 不显含时间 t 并且与哈密顿算符 Ĥ 对易，则其平均值不随时间变化，即 此时称物理量 A 是守恒量。例如：

• 能量是守恒量，因为体系的哈密顿量通常不显含时间。
• 自由粒子的能量、动量和角动量都是守恒量。（哈密顿算符仅包含动能项）
• 在中心力场中，粒子的动量不是守恒量，但L̂² 、 L̂_z 、 Ĥ是守恒量。

一组彼此独立且相互对易的算符构成一个力学量完全集，如果给定一组量子数之后能够完全确定体系的一个可能的状态。例如，在中心力场中，哈密顿算符 Ĥ、角动量平方 L̂² 和角动量分量 L̂_z 构成了一个力学量完全集，并且它们有共同的本征函数。这些对应的量子数被称为好量子数，参与对系统的描述。